重要提示：
请勿将账号共享给其他人使用，违者账号将被封禁！
题目内容
（请给出正确答案）
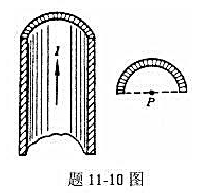
分析:微分半圆柱形金属薄片，对微分电流dI应用无限长载流直导线产生的磁场公式求解 。
并将场强矢量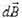
分解后再积分求解总的磁感应强度。注意利用场的对称性。
更多“在半径R=1cm的“无限长”半圆柱形金属薄片中，有电流I=5A自下而上地通过，如题11-10图所示。试求圆”相关的问题
第1题
试求圆柱轴线上任意一点P的磁感应强度B的大小及方向。
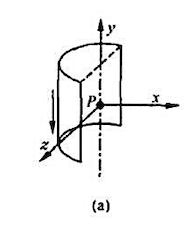
第7题
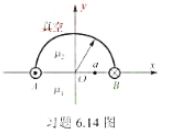
第8题
容器长L=2m,E点处压力表读数为9.8N/cm2.h=2m.试求:(1)作用在顶盖AB上的总压力;(2)作用在侧壁CD上的总压力的水平分力和垂直分力.
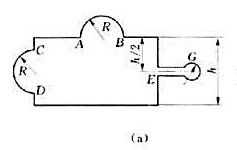
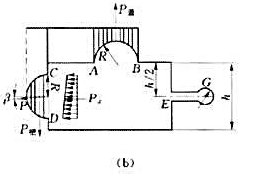
[例82]图
第10题
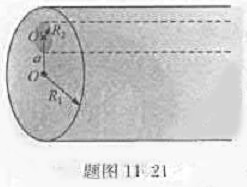
(1)圆柱轴线上的磁感应强度的大小;
(2)空心部分轴线上的磁感应强度的大小。
客服
TOP
警告：系统检测到您的账号存在安全风险
为了保护您的账号安全，请在“上学吧”公众号进行验证，点击“官网服务”-“账号验证”后输入验证码“”完成验证，验证成功后方可继续查看答案！
